블로그 옮겼습니다

문제 링크 N N; for(int i = 0; i > a; for(int j = 1; j * j = 2; i--){ if(!cnt[i]) continue; c[i] = (c[i] + cnt[i] * pow2[cnt[i] - 1]) % mod; for(int j = 2; j * j

$N,M\le{10^5}$인덱스 이외의 모든수는 ${10^6}$ 이하의 자연수 N개의 수로 이루어진 A[i] 가 주어지고, M개의 쿼리가 주어지는데 각 쿼리는 b, l, r 로 이루어지며구해야 할 것은 b의 약수들 중에 $A_l, A_{l+1}, \dots, A_r$ 들을 모두 나눌 수 없는 약수들의 수 이다.이 각 쿼리들의 결과를 모두 합한 값을 출력하는 문제이다.어차피 각 수는 10^6 이하이기 때문에 이런 배열을 하나 만들 수 있다.last[i] : i로 나눌 수 있는 최대 인덱스그럼 오프라인으로 각 쿼리를 r 로 오름 차순 정렬한뒤 하나하나 봐주면서 현재 쿼리의 r까지 A[i]의 약수들에 대해 last[약수] 를 i로 업뎃해준다. 그런뒤 b의 약수들에 대해 last[약수] 가 l보다 크..

http://codeforces.com/contest/535/problem/D 길이가 n인 어떤 문자열 s 가있고, 이 s안에서 k번 등장하는 어떤 패턴 p가 있다.패턴 p가 등장하는 위치를 오름차순으로 정렬한 sequence 에서 m개의 숫자로 이루어진임의의 subsequence 를 sub 이라고하자.입력으로 n, m, p, sub 가 주어질 때, 가능한 원래의 문자열 s의 가짓수를 구하는 문제이다.$1 \le n \le 10^6$$0 \le m \le n - |p| + 1$$1 \le |p| \le n$ 우선, 길이 n인 연속된 빈 칸을 생각해 보자 여기에 p가 등장하는 위치에 p를 넣고 난 뒤빈 칸의 개수를 x라고 할 때 $26^x$ 를 $10^9+7$ 로 나눈 나머지를 구하는 문..

문제 링크 $0\lt{N}\le{10^3}$$0\lt{K}\le{10^6}$문제는 간단하다. N개의 사람이 있고 K개의 경기가 있다.모든 경기는 적어도 한명은 참가되어야하지만 딱 한사람만 참가할 수 있다.각 사람은 적어도 한 경기는 해야하고 한 사람은 여러개의 경기를 할 수가 있다.이 때 경기가 배정되는 경우의 수를 구하는 문제이다. 우선 K가 10^6인건 훼이크라는 것을 알 수가 있다. 왜냐하면 K가 N보다 크면 모든 사람에게 적어도한경기씩 배정할 수가 없기 때문이다. 그렇기 때문에 K > N 이면 바로 0 을 출력하고 넘어간다면K > T; while(T--){ memset(dp,0,sizeof(dp)); dp[0][0] = 1; cin >> N >> K; if(K > N){ cout

문제 링크 $N\le{10^6}$자연수 N이 주어진다. N을 네개의 소수의 합으로 분리할 수 있으면 그 네개의 수를 출력하고불가능하면 -1을 출력하는 문제이다. 우선 골드바흐의 추측이라는 것이 있다. 2보다 큰 짝수는 무조건 두개의 소수의 합으로 나타낼 수 있다는 것이다.내가 알기론 이미 꽤 큰 수(적어도 PS에서 주어지는 입력의 범위보단 큰 수) 까지는컴퓨터로 일일이 돌려보아 증명이 되었다고 알고있다. 그러니까 맞다고 생각하고 풀면된다 ㅎㅎ일단 입력으로 주어진 N이 홀수일 때와 짝수일 때로 나누어 보자.만약 홀수라면 골드바흐의 추측을 적용하기 위해 이를 짝수로 만들어 줘야 하므로 우선 하나의 수를 빼야하는데너무 많이 빼면 2이하가 될 수도 있으므로 가장 적게 빼는게 최선이므로 가장 작은 홀수 소수..

문제 링크 $1\le{N}\le{10^5}$N 개의 음이 아닌 정수가 주어지고 부분 배열 A[i~j]중에 sum(i~j) * min(i~j) 가 가장 큰 것의 값을구하는 문제이다. 이 문제를 O(NlgN) 과 O(N) 이렇게 두가지 방법으로 풀어보았다.우선 첫번째로 O(NlgN) 에 푸는 방법이다.방법은 이렇다. 일단 잘 생각해보면 구간의 min 값이 정해졌다면 min값이 그 것으로 유지되는 한가장 많은 수를 더하는 것이 최적이라는 것이다. 그렇기 때문에 어떤 하나의 숫자 A[k] 부터 시작해서왼쪽, 오른쪽으로 시작한 수 A[k] 보다 더 작은 수가 나오기 전까지 쭉쭉 확장시켜보자.그럼 min(i~j)값이 A[k] 일 때의 최대 점수이다. 그렇다면 min(i~j) 값은 N개 각각의 정수가 될 수가 ..

문제 링크 $1\le{N, M, K}\le{300,000}$$1\le{a_i, p_i}\le{10^9}$M개의 구역이 있다. 각각의 구역은 N개의 국가중 하나에 의해 소유된다. N개의 국가는 각자 pi개의 운석 샘플을 가져가야 한다.유성이 K번 떨어진다. 유성이 한번 떨어질 때에는 특정 연속된 구간에 특정량이 떨어진다.li, ri, ai 로 표현될 수 있으며 구역은 원형이므로 li > ri 일 수도 있음에 유의한다. 유성이 어떤 국가에 속한 구역에 떨어지면 그 떨어진 개수만큼 해당 국가는 샘플을 습득할 수 있는 것이다.그렇다면 각 국가가 필요로 하는 샘플의 개수를 처음으로 충족하게 되는 건 몇 번째 유성이떨어졌을 때인지 구하는 문제이다. 즉, 답은 N개의 정수를 출력해야한다.naive 하게 생각해..

문제 링크 $1\le{N, M}\le{10^5}$$0\le{Q}\le{10^5}$이 문제는 N개의 노드가 있고, 각 노드는 M개의 그룹중 하나에 속한다. 그리고 총 Q개의 간선을 설치할건데1번부터 순차적으로 설치할것이다. 그럴 때에 각 그룹에 대해 그룹에 속한 노드들이 모두 하나의 컴포넌트로연결되는 최소 간선 번호를 구하는것이다. 그러므로 최종적으로 M개의 정수를 출력하면된다.Q번 간선까지 설치했는데도 모든 그룹 노드들이 연결되지않는다면 -1을 출력, 그리고 하나도 간선을 설치하지않아도 모두 연결되면 0을 출력하면된다. 일단 0을 출력하는 경우는 그룹에 속한 노드가 딱 하나만있는 경우밖에 없다. 그러므로 이경우만 따로 처리해주면 될 것이다. 일단 naive 하게 생각해보자. M개의 그룹에 대해서 ..

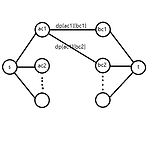
문제 링크 노드의 수가 100개 이하인 두개의 트리 g1, g2 가 주어진다. 두 트리의 루트 노드는 모두 1번 노드이다. 두 트리의 최대 공통 노드 수를 출력하는 문제이다. 쉽게 말해서 각 노드에 대해서 자식 노드들의 순서를 요리 조리 바꿔도 여전히 같은 트리이기 때문에 각 노드의 자식들의 순서를 요리 조리 바꿨을 때 두 트리중 모양이 일치하는 가장 노드가 많은 부분 트리의 노드 수를 구하는 문제이다. dp[a][b] : 트리 g1에서 노드 a를 루트로 하는 서브트리와, 트리 g2에서 노드 b를 루트로 하는 서브트리의 최대 공통 노드 수 라고 부분 문제를 정의하면 트리 dp 로 해결할 수가 있다. 그렇다면 부분 문제 테이블의 하나의 셀을 어떻게 채울까? 답은 MCMF 이다. dp[a][b] 에서 a의 ..

문제 링크 n, m, d (1 ≤ n ≤ 150000; 1 ≤ m ≤ 300; 1 ≤ d ≤ n).수직선에 1, 2, ..., n 의 장소가 있다. m 개의 폭죽이 임의의 시간과 장소에서 발사된다.주인공은 1초에 d만큼 이동할 수 있다. 시작 위치는 아무데서나 시작해도 된다.i번 폭죽이 발사될 때 주인공이 x 지점에 있을 때 얻게되는 행복은 $b_i - |a_i - x|$ 이다.이 때 모든 폭죽이 발사되고 난 후에 주인공이 얻은 행복의 양이 최대가 되도록 하고싶다.그 아랫줄부터는 m개의 폭죽의 대한 정보 ai, bi, ti 가 주어진다.ai, bi, ti (1 ≤ ai ≤ n; 1 ≤ bi ≤ 109; 1 ≤ ti ≤ 109) dp[i][j] : t_i 시간에 j 위치에 있을 때 최대 행복도\(dp[..