블로그 옮겼습니다
UVa OJ 11851 - Celebrity Split 본문
1≤N≤24
106≤P[i]≤4⋅107(0≤i<N)
맨션의 개수 N이 주어지고, 각 맨션의 가격 P[i] 가 주어진다. 두 사람이 이혼을 하는데 맨션을 나눠 가지려 한다.
각 맨션은 남자가 갖거나, 여자가 갖거나, 둘 다 안갖고 부동산에 팔거나 셋중 하나이다.
이 때 남자가 갖게되는 맨션들의 가격의 합과 여자가 갖게되는 맨션들의 가격의 합이 무조건 같도록
맨션을 나누고 싶다. 대신 가능한한 부동산에 파는 맨션의 가격을 최소화하고 싶다. 이 때 부동산에 팔아야하는
맨션들의 가격의 합을 구하는 문제이다.
일단 naive 하게 각 맨션이 여자가 가짐,남자가 가짐,부동산에 팜 셋중 하나니까 3가지의 경우의 수가 있고
N개의 맨션이 있으므로 O(3^N) 가지의 방법들을 모두 보면서 각 경우에 여자가 갖는 재산과 남자가 갖는 재산이
같은지만 비교해서 두 재산의 합을 전체 재산에서 뺀것이 최소가 되도록 답을 갱신해주면된다.
이건 시간복잡도가 3N 라서 너무 느리다. 왜냐하면 324는 매우 크기 떄문이다.
그럼 이것을 두개로 쪼개 보자. 왼쪽 맨션들의 그룹을 L, 오른쪽을 R이라고 하자.
각 그룹에 대해 모든 경우를 따지는 데에는 O(3N2) 이 걸리는데 이것은 3^12 는 50만정도 되므로
반띵에 대해 모든 경우를 따지는 것은 충분히 가능하다. 그럼 3진법으로 모든 경우에 대해
여자가 갖게 되는 재산과 남자가 갖게 되는 재산을 구한뒤 여자재산-남자재산 을 인덱스로 여자재산+남자재산으로 max
값으로 갱신해준다. 왜냐하면 왼쪽 그룹에서 두 사람의 재산의 차(부호 있음)와 오른쪽 그룹에서 두 사람의 재산의 차를
더해서 0이 되는 경우만이 두 사람의 각각의 전체 재산이 같아지기 때문에 여자재산-남자재산을 표시해두면
반대쪽 그룹에서 부호만 바꿔서 한번에 확인이 가능하기 때문이다. 그리고 재산차이가 같게 하는 경우가
여러개라면 두 사람의 재산이 최대가 되는 경우만 보면 되므로 max 갱신 시켜주는 것이다.
그럼 오른쪽그룹에서 모든 경우를 보며 이번엔 반대로 남자재산-여자재산을 map의 인덱스로 하는 곳이 0이 아니면
반대쪽에서 있었다는 거니까 왼쪽 반띵에서 나눈 두 사람의 재산의 합인 map의 value 와 지금 남자재산+여자재산과의
합을 구하면 남자재산과 여자재산이 같을 때 두 사람의 재산의 총합이 나온다. 이걸 전체 재산에서 빼면 부동산에
팔아야 하는 맨션들의 가격이 나오고 이것에 대해 답을 min 갱신 해주면 된다.
이렇게만 생각하면 끝.. 인줄알았는데 WA가 떠서 이유를 잘 살펴보니 왼쪽 그룹에 있는 모든 맨션들을 부동산에 팔면
여자재산 + 남자재산이 0이 되어 map 에 표시해줄 때 애초에 이런 경우가 없는 것과 구분할 수 없어서 그런거였다.
그렇기 때문에 오른쪽에서만 고르는 경우를 추가적으로 따져주자. 즉, 오른쪽에서 모든 경우에 대해
여자재산 = 남자재산인 경우 왼쪽그룹을 신경쓰지 말고 그냥 이걸로 답 갱신해준다. 아니면 map.find 를 하여
실제로 데이터가 있는지 없는지를 알 수 있으므로 바로 해결될 것이다.
그리고 각 테스트 케이스에서 map clear 잘해주고 sum = 0으로 초기화 잘해주자.... 이걸로 디버깅하는데 시간좀 듬 ㅠ
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 | #include <bits/stdc++.h> using namespace std; const int MOD = 1e9+7; const int INF = 0x3c3c3c3c; const long long INFL = 0x3c3c3c3c3c3c3c3c; int N; int price[30]; map<int, int> mp; int pow3[30]; int sum; int main() { pow3[0] = 1; for(int i = 1 ; i < 13; i++) pow3[i] = pow3[i-1]*3; while(1){ mp.clear(); sum = 0; scanf("%d",&N); if(!N) break; for(int i = 0 ; i < N; i++) scanf("%d", price+i), sum += price[i]; int ans = sum; int L = N/2; int R = (N+1)/2; for(int i = 0 ; i < pow3[L]; i++) { int A = 0, B = 0; for(int j = i, k = 0;j;j/=3, k++){ int sel = j%3; if(!sel) continue; else if(sel==1) A += price[k]; else B += price[k]; } mp[A-B] = max(mp[A-B], A+B); } for(int i = 0 ; i < pow3[R]; i++) { int A = 0, B = 0; for(int j = i, k = 0;j;j/=3, k++){ int sel = j%3; if(!sel) continue; else if(sel==1) A += price[L+k]; else B += price[L+k]; } if(mp[B-A] || A==B) ans = min(ans, sum - (mp[B-A] + A + B)); } printf("%d\n",ans); } return 0; } | cs |
'Algorithm > Problem Solving' 카테고리의 다른 글
| Topcoder SRM 519 Div1(Medium) RequiredSubstrings (0) | 2017.05.03 |
|---|---|
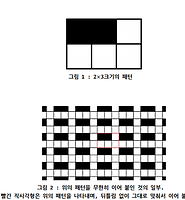
| 제 5회 kriiicon YZ(Young Zebra) (0) | 2017.05.03 |
| Topcoder SRM 528 Div1(Medium) SPartition (0) | 2017.05.03 |
| BOJ 10166번 관중석 (0) | 2017.05.03 |
| SCPC 2016 본선 A. 재활용 (0) | 2017.05.02 |