블로그 옮겼습니다
완전 순열(교란 순열) 본문
N 명의 사람이 각각 선물을 하나씩 준비해왔을 때 모두가 자신이 준비한 선물 이외의 선물을 갖도록 나눌 때
그 경우의수를 구하는 문제
1 2 3 4 5 다섯명의 사람이 있다고 가정하자.
맨 처음에 1번사람은 자신의 선물이 아닌 나머지 사람들의 선물, 즉 n-1 개의 선물을 가질 수 가 있다.
그럼 그중에 하나의 경우인 1번사람이 2번사람의 선물을 가질 때를 생각해보자.
그럼 2번사람이 받는 선물은 두가지 경우로 나뉜다.
첫번째, 1번사람의 선물을 갖는 경우. 그럼 1번 사람과 2번사람이 선물을 둘이 교환한 것과 같게 되므로
D[i] : i명의 사람이 자신의 선물을 안갖도록 선물을 교환하는 경우의수
일때, 교환한 두명을 제외한 나머지 n-2명에게 같은 행위를 반복하므로 D[n-2] 가 된다.
두번째, 1번 사람이 아닌 사람의 선물을 갖는 경우. 지금 선물을 받아야할 사람은 2,3,4,5 네명이고
남은 선물은 1,3,4,5 선물 이렇게 네개이다. 그럼 2번사람은 1번선물을 가지면 안되고
3번 사람은 3번 선물을, 4번사람은 4번 선물을, 5번사람은 5번 선물을 각각 가지면 안된다.
그 외에는 어떻게 분배하든 상관없다.
사실 k번 사람이 k번 선물을 가지면 안된다는 것은 너무나도 당연하지만 2번사람이 1번선물을 가지면 안된다는
것을 잘 생각해보면, 번호만 다를 뿐이지 x개의 선물을 각각 특정 사람에게 나누어지지 않도록 분배한다는 점에서
우리가 구하는 문제와 완전히 동일하다는 것을 알 수가있기 때문에 D[n-1] 이 된다는 것을 알 수가 있다.
그럼 결국
D[i] = (i-1) * (D[i-1] + D[i-2])
라는 점화식이 나오게 된다.
예제1: https://www.acmicpc.net/problem/1947
예제2: https://www.acmicpc.net/problem/14578
그런데 나는 이 교란순열이라는 것의 존재를 모를 때 약간 다르게 풀었다. 결국 비슷한 맥락이긴 한 것같은데
dp[i][j] : 앞으로 i명의 사람에게 선물을 나눠줘야하고,
특정 한 사람은 자신이 준비한 선물을 이미 누군가가 가져갔는지 여부 j
점화식은 소스코드로 대체한다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | #include <bits/stdc++.h> using namespace std; typedef long long ll; const int mod = 1e9; const int inf = 0x3c3c3c3c; const long long infl = 0x3c3c3c3c3c3c3c3c; int N; ll dp[1000003][2]; ll go(int pos, int o){ if(pos==1) return o; ll& cache = dp[pos][o]; if(cache != -1) return cache; ll ret = (pos-1) * go(pos-1,1) % mod; if(o) ret = (ret + go(pos-1,0)) % mod; return cache = ret; } int main() { memset(dp,-1,sizeof(dp)); cin >> N; cout << go(N,0); return 0; } | cs |
'Algorithm > Memo &Tips' 카테고리의 다른 글
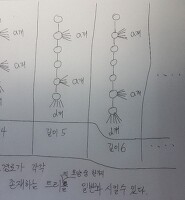
| 길이가 K인 단순경로가 N개 존재하는 트리만들기 (0) | 2017.06.29 |
|---|---|
| 서로 다른 두 수의 최소합 O(n) 에 구하기 (0) | 2017.06.27 |
| 어떤 소수를 정수로 만들기 위해 곱해야하는 최수 정수 구하기 (0) | 2017.05.26 |
| 꼭 알아야 하는 이항계수 공식 (0) | 2017.05.23 |
| 중복없이 서로 다른 답들의 수를 세는 방법 (0) | 2017.05.19 |